 |
Even better low-pass filters for transmitters
27 November 2016 | by The last issues of QEX have featured two interesting articles by Gary Cobb, G3TMG. He outlines the advantage of using Zolotarev designs for the harmonic suppression filters of transmitters, giving even better suppression of the second harmonic than the more common Chebyshev or quasi-elliptic filters.
 |
| Chebyshev low-pass filter from the GQRP data sheet (issue 1) |
My interest in this was triggered by the test of the Ultimate 3 QRSS/WSPR kit from QRP Labs in the Nov 2016 QST. The review was positive overall, but it was remarked that the harmonic suppression does not meet FCC requirements (-43 dBc or better). I am not sure whether this is due to PCB layout issues, or if better filters can alleviate it, but I note that the design uses the simplest filter of the ones I have listed here.
The evolution of filters for use for harmonic suppression follows at least these three steps:
- Chebyshev type I filters with equiripple in the passband and a monotonically falling, maximally flat stopband. A 7-pole version with three inductors and four capacitors in a pi-network has been around for a while, in e.g. the old recommendation from the GQRP club. It was based on the QST paper “Low-pass filters for amateur radio transmitters,” Ed Wetherhold, W3NQN, Dec. 1979. Two designs for a 20 m filter were given there:
1) Max. ripple in passband: 0.00731 dB, attenuation at 28 MHz: 40.7 dB
1) Max. ripple in passband: 0.00960 dB, attenuation at 28 MHz: 34.5 dB 
Second-harmonic optimized low-pass filter from the
GQRP data sheet (issue 2)An improved stopband was the topic of W3NQN’s article “Second-harmonic optimized low-pass filters” in QST Feb. 1999. Here there is one additional capacitor as the central inductor is made into a parallel resonance which gives a zero in the stopband, based on an idea by Jum Tonne, WB6BLD. The design goal is that this zero should be at the second harmonic frequency. W3NQN proposed to call this a Chebyshev filter with a zero (CWAZ) filter, but it is more correct to call it a quasi- or pseudo-elliptic filter as remarked by G3TMG. It increases the attenuation at the second-harmonic in the 20 m design to better than 60 dB. This design is the basis for the current (Issue 2) G-QRP technical sheet. This would also be interesting to test in the QRP Labs Ultimate 3 transmitter kit.
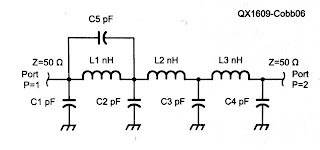
Zolotarev low-pass filter from the Nov/Dec 2016 QEX article G3TMG in the new QEX articles has noticed that the passband is over-specified in the above filters as the lower 60% or so of the passband is unused. The Zolotarev design allows for more passband ripple in this part where it does not matter. The advantage is even better stopband attenuation. A measured example for a 60 m filter has a passband ripple of 0.17 dB and a stopband attenuation at the second harmonic of 71 dB. This filter has the same component count as the previous one, but the filter is no longer symmetric like the two previous ones. The increase in second-harmonic suppression is not as great as the going from the first filters to the second, but should still be worth the effort.
- Gary Cobb, G3TMG, Zolotarev low-pass filter design, QEX, July/Aug 2016.
- Gary Cobb, G3TMG, A more efficient low-pass filter, QEX, Nov/Dec 2016.
One Response to “Even better low-pass filters for transmitters”
 Ham Radio Deluxe |
 Ham Radio Prep |
 KB3IFH QSL Cards  Hip Ham Shirts  HamRadioAuctions Reliance Antennas Enigma Shop |  morseDX  Ni4L Antennas  R&L Electronics antennas.us Ears to Our World |
- Matt W1MST, Managing Editor
Elliptic filters are sometimes referred to as Cauer or Zolotarev filters. From memory, elliptic filters have the steepest passband to stopband attenuation slope, higher than a Chebyshev filter (and hence higher than a Butterworth filter). The trade-off with elliptic filters is higher equal ripple in both the passband and stopband.
The elliptical filter transfer function coefficients can be adjusted to optimize an equiripple null for a given frequency, such as a second or third harmonic. But the process is tedious at the design stage – even more so at the build stage.
Forget about using an optimized passive elliptic filter in a production design, it is too intolerant. It is almost always cheaper, faster, and easier to use a tolerant filter design and increase the filter order.
Digital filters are a different matter. In fact there are a number of so-called “optimal” Zolotarev Finite Impulse Response (FIR) digital filters that have seen.
Some people are obsessed with tweaking passive filters, especially elliptical filters. I call it beating a dead cat… “If you catch yourself beating a dead cat, then there was something fundamentally wrong with the cat to start with”. 73’s David